大数加法#
给定两个字符串形式的非负整数num1和num2，计算它们的和并以字符串形式返回。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
string addStrings(string num1, string num2) {
int i = num1.size() - 1, j = num2.size() - 1, carry = 0;
string res("");
while(i >= 0 || j >= 0) {
int x = i>=0? num1[i]-'0': 0;
int y = j>=0? num2[j]-'0': 0;
int t = x + y + carry;
carry = t/10;
res.insert(0, to_string(t%10));
i--, j--;
}
if (carry) res.insert(0, "1");
return res;
}
|
大数乘法#
给定两个字符串形式的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，计算它们的乘积并以字符串形式返回。
[解析]：本题有两种思路：
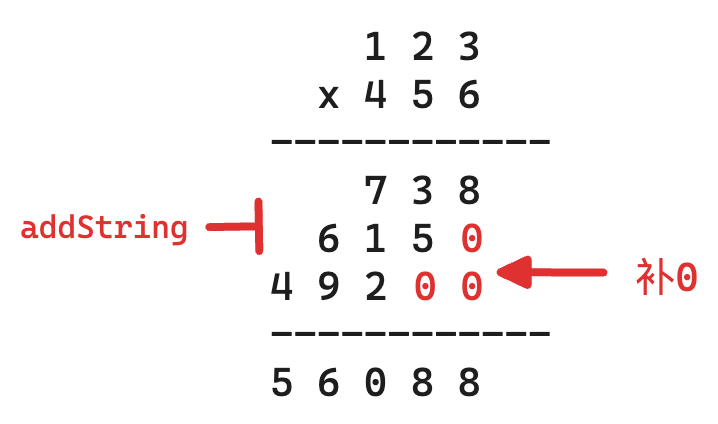方法1：模拟竖式计算
|
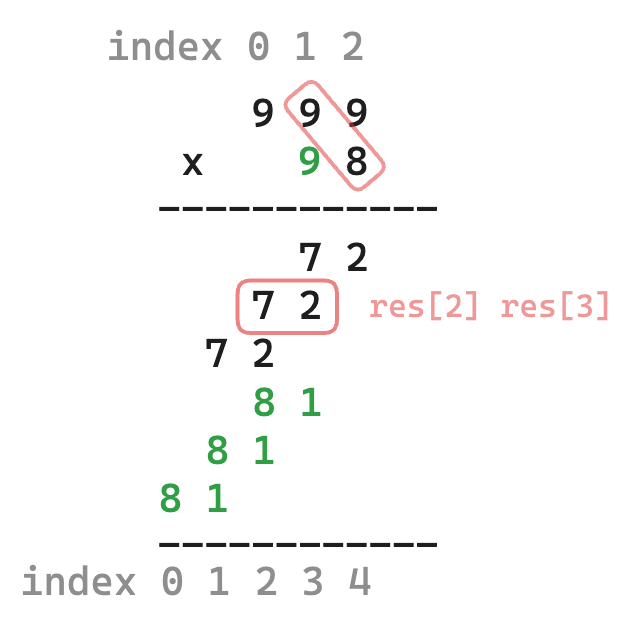方法2：乘法规律计算
|
-
做加法：模拟竖式计算，从右往左遍历乘数，将乘数的每一位与被乘数相乘得到对应的结果，再将每次得到的结果累加（累加时使用大数加法 addString 的思路）；
-
做乘法：通过两数相乘时，乘数某位与被乘数某位相乘，与产生结果的位置的规律来完成。具体规律如下：
代码 方法1🤔
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
string multiply(string num1, string num2) {
if (num1 == "0" || num2 == "0") return "0";
int l1 = num1.size() - 1, l2 = num2.size() - 1;
string res("0");
for (int i = l1; i >= 0; i--) {
string curr(l1-i, '0'); // 补0
int x = num1[i] - '0', carry = 0;
for (int j = l2; j >= 0; j--) {
int y = num2[j] - '0';
int t = x * y + carry;
carry = t / 10;
curr.insert(0, to_string(t%10));
}
if (carry) curr.insert(0, to_string(carry));
res = addStrings(res, curr);
}
return res;
}
string addStrings(string num1, string num2) {
int i = num1.size() - 1, j = num2.size() - 1, carry = 0;
string res("");
while(i >= 0 || j >= 0) {
int x = i>=0? num1[i]-'0': 0;
int y = j>=0? num2[j]-'0': 0;
int t = x + y + carry;
carry = t/10;
res.insert(0, to_string(t%10));
i--, j--;
}
if (carry) res.insert(0, "1");
return res;
}
|
代码 方法2🤔
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
string multiply(string num1, string num2) {
if (num1 == "0" || num2 == "0") return "0";
int l1 = num1.size(), l2 = num2.size();
vector<int> res(l1+l2, 0);
for (int i = l1 - 1; i >= 0; i--) {
int x = num1[i] - '0';
for (int j = l2 - 1; j >= 0; j--) {
int y = num2[j] -'0';
int sum = res[i+j+1] + x*y;
res[i+j+1] = sum % 10;
res[i+j] += sum / 10; // res[i+j] 可能大于等于 10，下一轮计算时会进行累加，即第9行代码
}
}
string ans;
for (int i = 0; i < l1+l2; i++) {
if (i == 0 && res[i] == 0) continue;
ans += res[i] + '0';
}
return ans;
}
|
位运算#
负二进制转换#
https://leetcode.cn/problems/convert-to-base-2/
负二进制数相加#
https://leetcode.cn/problems/adding-two-negabinary-numbers/solutions/2273578/fu-er-jin-zhi-shu-xiang-jia-by-leetcode-nwktq/