链表定义与基础操作#
链表的结点定义#
1
2
3
4
5
6
7
|
struct ListNode {
int val;
ListNode *next;
ListNode(): val(0), next(nullptr) {}
ListNode(int x): val(x), next(nullptr) {}
ListNode(int x, ListNode *next): val(x), next(next) {}
};
|
建立单链表#
建立单链表可以使用尾插法和头插法,为了方便操作这里申请了一个“dummy_head”结点,指向链表头部。使用头插法建立的链表和输入序列相反,例如输入:“1 2 3 4 5”,建立的链表为:5→4→3→2→1。
尾插法#
1
2
3
4
5
6
7
8
9
10
11
|
ListNode *create_linklist_tail_insert() {
ListNode *dummy_head = new ListNode(-1);
ListNode *node = dummy_head;
int t;
while (cin >> t) {
node->next = new ListNode(t);
node = node->next;
}
return dummy_head->next;
}
|
头插法#
1
2
3
4
5
6
7
8
9
10
11
12
|
ListNode *create_linklist_front_insert() {
ListNode *dummy_head = new ListNode(-1);
ListNode *node = nullptr;
int t;
while(cin >> t) {
node = new ListNode(t);
node->next = dummy_head->next;
dummy_head->next = node;
}
return dummy_head->next;
}
|
合并两个有序单链表#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
ListNode *merge_two_ordered_linklist(ListNode *l1, ListNode *l2) {
if (l1 == nullptr) return l2;
if (l2 == nullptr) return l1;
ListNode *dummy_head = new ListNode(-1);
ListNode *node = dummy_head;
while(l1 && l2) {
if (l1->val < l2->val) {
node->next = l1;
l1 = l1->next;
} else {
node->next = l2;
l2 = l2->next;
}
node = node->next;
}
node->next = l1? l1: l2;
return dummy_head->next;
}
|
判断链表是否有环#
通过快慢指针有效解决此类问题。快指针每次相对慢指针多走一步,当快慢指针都在链表的环内时,快指针最多多走一圈能追上慢指针。
1
2
3
4
5
6
7
8
9
10
|
bool hasCycle(ListNode *head) {
if (head == nullptr || head ->next == nullptr) return false;
ListNode *slow = head, *fast = head;
while(fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
if (slow == fast) return true;
}
return false;
}
|
进阶:找到环形链表的入口结点#
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
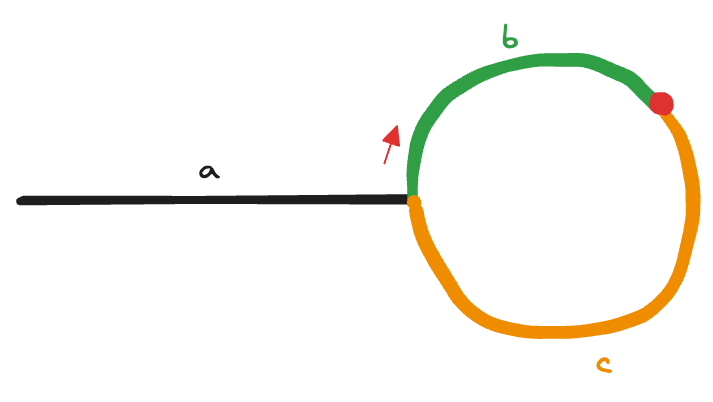
[解析]:我们找到快慢指针 $f,s$ 相遇的环内结点,此时让指针 $t$ 从链表头部出发,让 $s$ 和 $t$ 同步移动,当 $s$ 和 $t$ 相遇时,该处即为环形链表的入口结点。证明如下:
 证明
证明
设链表中环外部分的长度为 $a$,慢指针进入环后,又走了 $b$ 的距离与快指针相遇。此时,设快指针已经走完了环的 $n$ 圈,因此它走过的总距离为 $a+n(b+c)+b$。
又因为快指针走过的距离一定为慢指针的两倍,所以有:
\begin{equation}
\begin{aligned}
&a+n(b+c)+b=2(a+b)\\
\Rightarrow\quad &a=c+(n-1)(b+c)
\end{aligned}
\end{equation}
我们发现:从相遇点到入环点的距离加上 $n−1$ 圈的环长,恰好等于从链表头部到入环点的距离,所以 $s$ 和 $t$ 会在环形链表的入口结点相遇。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
ListNode *detectCycle(ListNode *head) {
if (head == nullptr || head->next == nullptr) return nullptr;
ListNode *s = head, *f = head, *t = head;
while(f && f->next) {
s = s->next;
f = f->next->next;
if (f == s) break;
}
if (f != s) return nullptr; // 无环
while(t != s) {
t = t->next, s = s->next;
}
return t;
}
|
证明