Floyd算法

Floyd 算法（Floyd-Warshall algorithm）是解决加权图中顶点间的最短路径算法之一，使用范围：无负权回路即可，边权可以为负值，运行一次算法即可求得任意两点间最短路。

其状态转移方程如下（结点 $i$ 借助 $k$ 更新到 $j$ 的距离）：

$$G[i][j]=min(G[i][j],\ G[i][k]+G[k][j]);$$

$G[i][j]$ 表示顶点 $i$ 到 $j$ 的最短距离，$k$ 是枚举的借助的点，时间复杂度：$O(n^3)$。

初始状态：

  1. 如果 $i$，$j$ 之间有边，$G[i][j] = len$；
  2. 如果 $i == j$，$G[i][j] = 0$；
  3. 其余情况，$G[i][j] = ∞$。

注意：

需要判断 $i → k$ 以及 $k → j$ 是否真的有边，如果没有的话要进行特判（因为如果 $len_{i→k}=∞,\ len_{k→j}=-1,\ len_{i→j}=∞$，此时不应该更新 $G[i][j]$）。

模版： 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

// 结点编号 0 - n-1
// edges[i] = [u, v, w] 表示有一条从 u 到 v 权值为 w 的边
void floyd(int n, vector<vector<int>>& edges) {
    int G[n][n];
    // 初始化
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            G[i][j] = (i==j)? 0: INT_MAX;
        }
	}
    // 建图
    for (auto e : edges) {
        G[e[0]][e[1]] = e[2];
    }
    
    for (int k = 0; k < n; k++) {  // 穷举所以可能被借助的点
        for (int i = 0; i < n; i++) {  // 穷举所有的起点
            for (int j = 0; j < n; j++) {  // 穷举所有的终点
                if (G[i][k] != INT_MAX && G[k][j] != INT_MAX) {
                    G[i][j] = min(G[i][j], G[i][k] + G[k][j]);
                }
            }
        }
    }
}

例题：课程表 IV

Dijkstra算法

Dijkstra 算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径，即图的单源最短路径问题。它的主要特点是以起点为中心向外层层扩展（广度优先遍历思想），直到扩展到终点为止。

Dijkstra 算法时间复杂度为 $O(n^2)$，使用优先队列优化的 Dijkstra 算法时间复杂度可降低至 $O((m+n)\thinspace log\thinspace n)$，其中 $n=|V|$，$m=|E|$。

需要注意的是 Dijkstra 算法适用于有环图，但不能有效处理带负权边的图，如果边权是负数情况，则应该使用 Bellman-Ford 算法和 SPFA 算法。

算法思想：

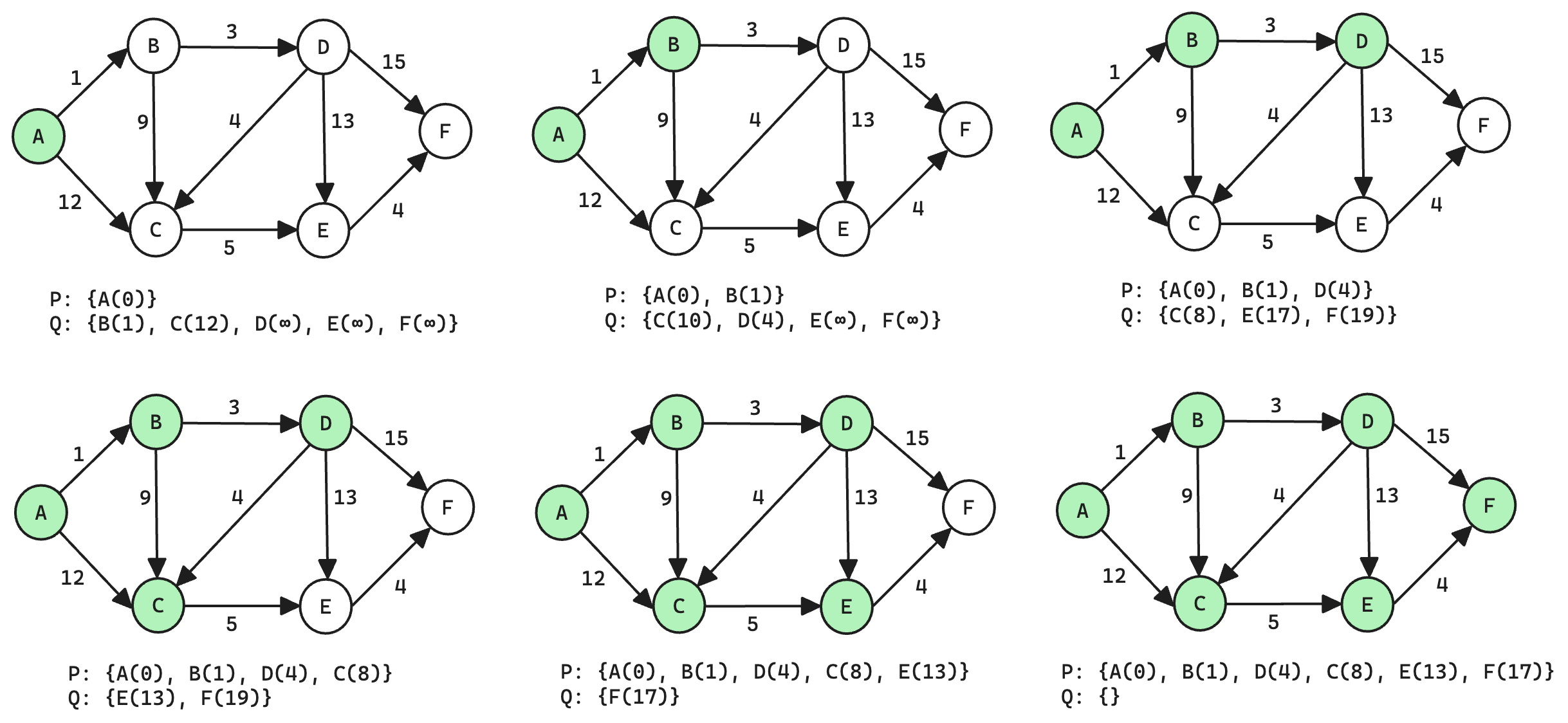Dijkstra 算法流程
  1. 在一个图中，把所有顶点分为两个集合 $P$，$Q$（$P$ 为最短路径集合，$Q$ 为待选集合），用 $dis$ 数组保存源点到各个顶点的最短路径（到自身为0）；
  2. 初始化 $P$ 集合，就是加入源点到该集合，并在 $vis$ 数组标记（代码中的 vis[st] = 1），那么 $Q$ 集合就是剩下的顶点构成了；
  3. 在 $Q$ 集合中找到这样一个顶点：源点到该顶点（记为 $curr$）的路径最短，把该点加入 $P$ 集合，列出以 $curr$ 为起点的所有边（终点记为 $t$），判断从源点到每一个 $t$ 顶点（因为以 $curr$ 为起点的边有多个）经过 $curr$ 顶点的路径是否会变小，更新 $dis[t]$ 的值；
  4. 重复步骤3，直到 $Q$ 集合为空，算法结束，此时 $dis$ 数组就存储了从源点到各个顶点的最短路径。

Dijkstra算法模版

代码 时间复杂度：O(n^2) 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

#include <bits/stdc++.h>
using namespace std;

// n个结点 m条有向边 源点st
// vis[i] = true/false 表示在 P/Q 集合
// dis[i] 保存了从源点到其他点的距离
int n, m, st;
bool vis[105];
int e[105][105], dis[105];

void dijkstra(int st) {
    // 初始化dis数组
    memset(dis, 0x3f, sizeof(dis));
    dis[st] = 0;

    for (int i = 1; i <= n; i++) {  // loop n rounds
        int curr = -1, minDis = 0x3f3f3f3f;
        for (int j = 1; j <= n; j++) {  // 找到未访问的最小距离
            if (!vis[j] && dis[j] < minDis) {
                minDis = dis[j];
                curr = j;
            }
        }
        if (curr == -1) break;

        vis[curr] = true;
        for (int t = 1; t <= n; t++)
            if (!vis[t]) dis[t] = min(dis[t], dis[curr] + e[curr][t]);
    }
}

int main() {
    cin >> n >> m >> st;
    int x, y, cost;
    // 初始化图结构
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            if (i == j) e[i][j] = 0;
            else e[i][j] = 0x3f3f3f3f;
        }
    }
    // 输入并构建邻接矩阵
    for (int i = 0; i < m; i++) {
        cin >> x >> y >> cost;
        e[x][y] = cost;
    }
    dijkstra(st);
    for (int i = 1; i <= n; i++) cout << dis[i] << " "; cout << endl;
    return 0;
}

/*
6 9 1
1 2 1
1 3 12
2 3 9
2 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4
 */

优先队列优化的Dijkstra算法

使用优先队列（小根堆）维护，能在 $O(1)$ 时间内找到未访问的最小距离（curr_w）和对应的结点（curr）。

代码 时间复杂度：O((n+m) log n) 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

#include <bits/stdc++.h>
using namespace std;

struct edge{
    int to, w;  // 结点编号 源点到该结点的最短距离
    edge(int _to, int _w): to(_to), w(_w) {}
    // 运算符重载 让priority_queue<edge>为小顶堆
    bool operator < (const edge& x) const { return w > x.w; }
};

// n个结点 m条有向边 源点st
// vis[i] = true/false 表示在 P/Q 集合
// dis[i] 保存了从源点到其他点的距离
// 优先队列维护的是Q集合，可以在O(1)时间内找到未访问的最小距离
int n, m, st, dis[105];
bool vis[105];
vector<edge> G[105];
priority_queue<edge> q;

void dijkstra(int st){
    // 初始化dis数组
    memset(dis, 0x3f, sizeof(dis));
    dis[st] = 0;
    q.emplace(st, 0);  // 初始源点在Q集合，从st到st的最短距离为0

    while(!q.empty()) {
        auto [curr, curr_w] = q.top(); q.pop();
        if(vis[curr]) continue;  // P集合已经扩散过了
        vis[curr] = true;

        for (auto [t, t_w] : G[curr]) {
            if (dis[t] > dis[curr] + t_w) {
                dis[t] = dis[curr] + t_w;
                q.emplace(t, dis[t]);  // 加入P集合
            }
        }
    }
}

int main() {
    cin >> n >> m >> st;
    int x, y, cost;
    for (int i = 0; i < m; i++) {
        cin >> x >> y >> cost;
        G[x].emplace_back(y, cost);
    }
    dijkstra(st);

    for (int i = 1; i <= n; i++) cout << dis[i] << " ";
    cout << endl;
    return 0;
}

例题

例1：Leetcode 743. 网络延迟时间

代码 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

class Solution {
public:
    typedef pair<int, int> PII;
    vector<PII> G[102];
    bool vis[102];
    int dis[102];
    priority_queue<PII, vector<PII>, greater<PII>> q;

    void dijkstra(int st) {
        // init dis[]
        memset(dis, 0x3f, sizeof(dis));
        dis[st] = 0;
        q.emplace(0, st);  // 注意这里的顺序是(距离, 结点编号)

        while(!q.empty()) {
            auto [curr_w, curr] = q.top(); q.pop();
            if (vis[curr]) continue;
            vis[curr] = true;

            for (auto [t, t_w] : G[curr]) {
                if (dis[curr] + t_w < dis[t]) {
                    dis[t] = dis[curr] + t_w;
                    q.emplace(dis[t], t);
                }
            }
        }
    }

    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        for (auto v : times) G[v[0]].emplace_back(make_pair(v[1], v[2]));
        dijkstra(k);
        int res = 0;
        return ((res = *max_element(dis+1, dis+n+1)) == 0x3f3f3f3f)? -1: res;
    }
};

例2：LeetCode 1334. 阈值距离内邻居最少的城市

[解析]：建双向图，跑 n 遍 Dijkstra 算法。

代码 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

class Solution {
public:
    typedef pair<int, int> PII;
    vector<PII> G[102];
    int dis[102][102];  // dis[i][] 表示源点为 i 的 dis 数组
    bool vis[102];

    void dijkstra(int st) {
        priority_queue<PII, vector<PII>, greater<PII>> q;
        memset(vis, 0, sizeof(vis));
        memset(dis[st], 0x3f, 102 * sizeof(int));
        dis[st][st] = 0;
        q.emplace(0, st);
        while (!q.empty()) {
            auto [curr_w, curr] = q.top(); q.pop();
            if (vis[curr]) continue;
            vis[curr] = true;
            for (auto [t, t_w] : G[curr]) {
                if (dis[st][t] > dis[st][curr] + t_w) {
                    dis[st][t] = dis[st][curr] + t_w;
                    q.emplace(dis[st][t], t);
                }
            }
        }
    }
    
    // 从 city_i 出发，路径距离小于等于 distanceThreshold 的城市数量
    int cityCount(int i, int n, int distanceThreshold) {
        int res = 0;
        for (int j = 0; j < n; j++) {
            if (dis[i][j] <= distanceThreshold) ++res;
        }
        return res - 1;
    }

    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        for (auto v : edges) {
            G[v[0]].emplace_back(make_pair(v[1], v[2]));
            G[v[1]].emplace_back(make_pair(v[0], v[2]));
        }
        int res = 0, cnt = INT_MAX;
        for (int i = 0; i < n; i++) {
            dijkstra(i);
            if (cityCount(i, n, distanceThreshold) <= cnt) {
                cnt = cityCount(i, n, distanceThreshold);
                res = i;
            }   
        }
        return res;
    }
};

例3：Leetcode 1786. 从第一个节点出发到最后一个节点的受限路径数

[解析]：优化的 Dijkstra 算法 + 动态规划。

代码 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

class Solution {
public:
    vector<pair<int, int>> G[20002];
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
    bool vis[20005];
    int dis[20005];

    void dijkstra(int st) {
        memset(dis, 0x7f, sizeof(dis));
        dis[st] = 0;
        q.emplace(make_pair(0, st));

        while(!q.empty()) {
            auto [curr_w, curr] = q.top(); q.pop();
            if (vis[curr]) continue;
            vis[curr] = true;
            for (auto [t, t_w] : G[curr]) {
                if (dis[t] > dis[curr] + t_w) {
                    dis[t] = dis[curr] + t_w;
                    q.emplace(make_pair(dis[t], t));
                }
            }
        }
    }

    int countRestrictedPaths(int n, vector<vector<int>>& edges) {
        for (auto e : edges) {
            G[e[0]].emplace_back(make_pair(e[1], e[2]));
            G[e[1]].emplace_back(make_pair(e[0], e[2]));
        }
        dijkstra(n);

        vector<long long> dp(n + 1, 0);
        dp[n] = 1LL;
        // 构建索引数组，按照dis从小到大排列
        vector<int> idx(n+1);
        for (int i = 1; i <= n; i++) idx[i] = i;
        sort(idx.begin(), idx.end(), [&](const int i, const int j) { return dis[i] < dis[j]; });
        for (int i : idx) {
            for (auto [to, w] : G[i]) {
                if (dis[i] > dis[to]) {
                    dp[i] += dp[to];
                    dp[i] %= 1000000007;
                }
            }
            if (i == 1) break;  // 剪枝，比1的距离还大的点，最短路径一定不会经过他们，不用考虑
        }
        return dp[1];
        return 0;
    }
};

拓扑排序

拓扑排序（Topological sort）是在 DAG（Directed Acyclic Graph, 有向无环图）上找到一个可以执行的线性顺序。图上存在拓扑序列与图是 DAG 之间形成充分必要条件。

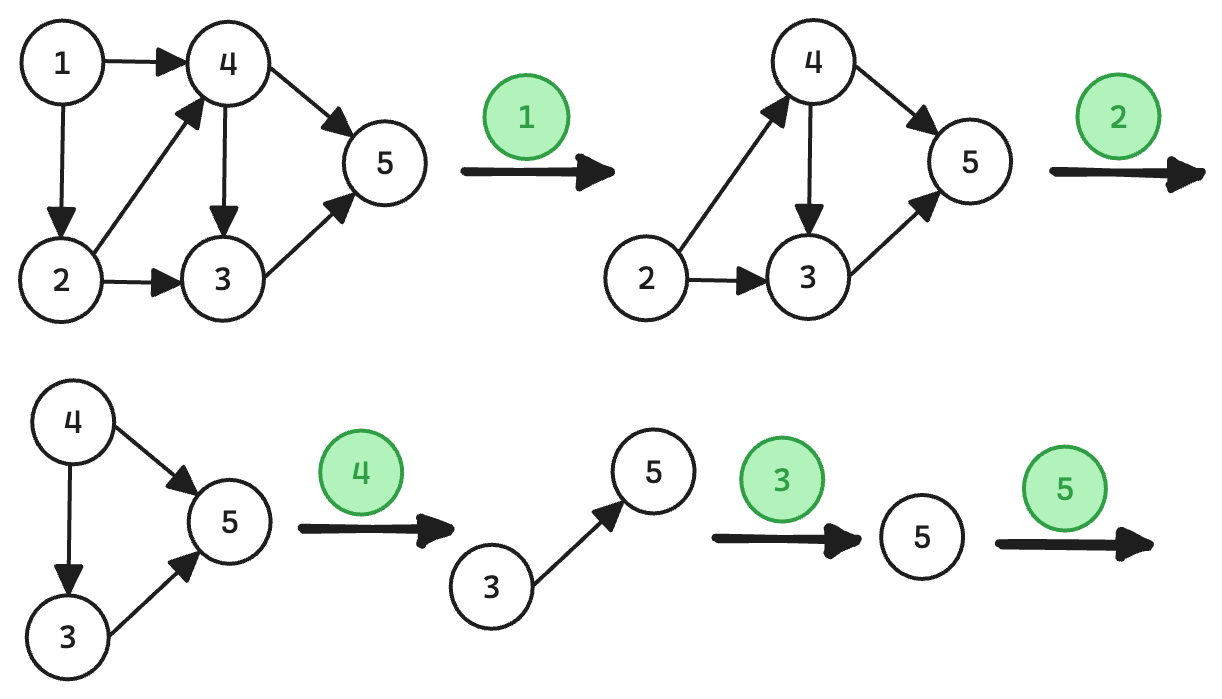拓扑排序

一种比较常用的拓扑排序方法：

  1. 从 DAG 中选择一个没有前驱（即入度为0）的顶点并输出；
  2. 从图中删除该顶点和所有以它为起点的有向边；
  3. 重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。

对应的算法步骤为：

  1. 每次从入度为 0 的结点开始，加入队列。入度为 0 ，表示没有前置结点；
  2. 处理入度为 0 的结点，把这个结点指向的结点的入度 -1；
  3. 重复 1 和 2，如果队列都处理完毕，但是和总结点数不符，说明有些结点形成环。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

/*
M = {{0,1}, {0,3}, {1,3}, {1,2}, {3,2}, {3,4}, {2,4}}

0 → 3 ↘︎
↓ ↗ ↓  4 
1 → 2 ↗ 

n = 5 表示编号 0-4 共 5 个结点
*/
vector<int> topologicSort(vector<vector<int>>& M, int n) {
    vector<int> inDegree(n, 0);  // 结点入度
    vector<vector<int>> G(n, vector<int>()); // 存储图 G[a] = {x, y} 表示 a->x, a->y
    queue<int> q;  // 存储入度为 0 的结点
    vector<int> res;
    
    // 存储图和节点入度
    for (auto v : M) {
        G[v[0]].emplace_back(v[1]);
        inDegree[v[1]]++;
    }
    // 入度为0的结点入队
    for (int i = 0; i < n; i++) {
        if (inDegree[i] == 0) q.push(i);
    }
    // 处理入度为 0 的结点，把这个结点指向的结点的入度 -1
    while(!q.empty()) {
        int st = q.front();
        q.pop();
        res.emplace_back(st);
        for (auto to : G[st]) {
	        if(--inDegree[to] == 0) q.push(to);            
        }
    }
    return (res.size() == n)? res: vector<int>{};
}

例题

例1：Leetcode 210. 课程表 II

代码 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        vector<int> inDegree(numCourses, 0); 
        vector<vector<int>> G(numCourses, vector<int>());
        for (auto v : prerequisites) {
            inDegree[v[0]]++;
            G[v[1]].emplace_back(v[0]);
        }

        queue<int> q;
        for (int i = 0; i < numCourses; i++) {
            if (inDegree[i] == 0) q.push(i);
        }

        vector<int> res;
        while(!q.empty()) {
            int node = q.front();
            q.pop();
            res.emplace_back(node);
            for (auto i : G[node]) {
                if (--inDegree[i] == 0) q.push(i);
            }
        }

        return (res.size() == numCourses)? res: vector<int>();
    }
};